Enter this into the Superscope module:
|
Init
|
n = 50;
|
|
On Beat
|
|
|
Per Frame
|
|
|
Per Point
|
x = i*2-1+.5*v;
y = x-v;
y = -y;
|
The Breakdown
- n = 50;
- This sets the number of points to define at 50. The higher n is, the more detailed the scope is.
- x = i*2-1+.5*v;
- The first part of this equation (i*2-1) is used to stretch out the x values and shift them over to the left.
This is done because if we only use i, without multiplying or subtracting, we only get x-values between 0 and 1.
By multiplying by two and shifting it over one, we get values from -1 to 1, for the whole AVS Window. The second part
(+.5*v) makes it so we get horizontal vibration.
- y = x-v;
- This is where we define y in terms of x, as we would for any linear equation. By stating y = x, we create a diagonal line
with a slope of 1. Also, since we're expressing y in terms of x, and x includes vibration (.5*v), we have to subtract this vibration to create
vibration in y. By subtracting v, we remove the value of the x vibration (.5*v), and create vibration in y (-.5*v). You could also think of this
as y = (x-.5*v)-.5*v; .
Note: Because of the shape of this graph, the v values for x and y have to have the opposite sign of each other (- and +), or vibration won't
be displayed.
- y = -y;
- This inverts the y values so that they behave as they would if the top were 1 and the bottom were -1, instead of the
opposite (see the Window tutorial).
Other Info
This may seem like a lot to think about to generate a simple line. Though really, the line's graph is easy enough, but the vibration
is a bit tricky in this case, mostly because of the shape of the graph.
Along with this superscope module, don't forget to use a fadeout or blur from the +>Trans menu, or you'll end up with
little more than a white blob.
Downloads
Making a Line tutorial and demonstration AVS Preset.
|
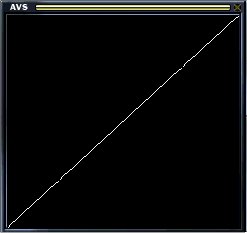
in action
|


