Even though the superscope is defined parametrically, we can use Polar equations in the superscope by using the definitions
of x, y, and r along with the polar equation, d.
Enter this into the superscope:
|
Init
|
n = 50;
|
|
On Beat
|
|
|
Per Frame
|
|
|
Per Point
|
d = .75+.5*v;
r = i*2*3.14159;
x = cos(r)*d;
y = sin(r)*d;
|
The Breakdown
- n = 50;
- This sets the number of points to define at 50. The higher n is, the more detailed the scope is.
- d = .75+.5*v;
- Here's where the polar equation is, which displays a circle at the polar value of d = .75, and vibrates around the
shape of the circle.
- r = i*2*3.14159;
- This allows all of the circle to be displayed, as it stretches i over all 2*pi of the polar equation.
- x = cos(r)*d;
y = sin(r)*d;
- These two definitions are what allows the polar equation to be displayed. By multiplying the parametric equation for a
circle by the value of the polar equation (d), the polar graph is displayed.
Other Info
Along with this superscope module, don't forget to use a fadeout or blur from the +>Trans menu, or you'll end up with
little more than a blob.
Though the variable d is used in this tutorial, d is not one of the default variables. Thus, you could use any variable you
wish in the place of d. Nearly any letter (or combination of numbers and letters) could be used aside from the defaults, which are
h, i, n, v, w, x, y, red, blue, and green. The same is true of r, which is used in this tutorial to allow more than the first radian
of the graph to be displayed.
Downloads
Polar Circle tutorial and demonstration AVS preset.
|
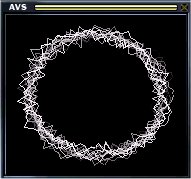
d = .75+.5*v;
r = i*2*3.14159;
x = cos(r)*d;
y = sin(r)*d;
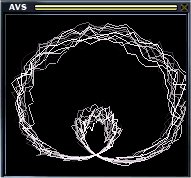
d = -sin(r)-.5+.2*v;
r = i*2*3.14159;
x = cos(r)*d;
y = sin(r)*d+.75;

r = i*7*3.14159;
d = .05*r+v*0.1;
x = cos(r)*d;
y = sin(r)*d;
|


